问题描述: 提供一些以数字为 id 的任务(task)，这些任务存在如下图所示的依赖关系:
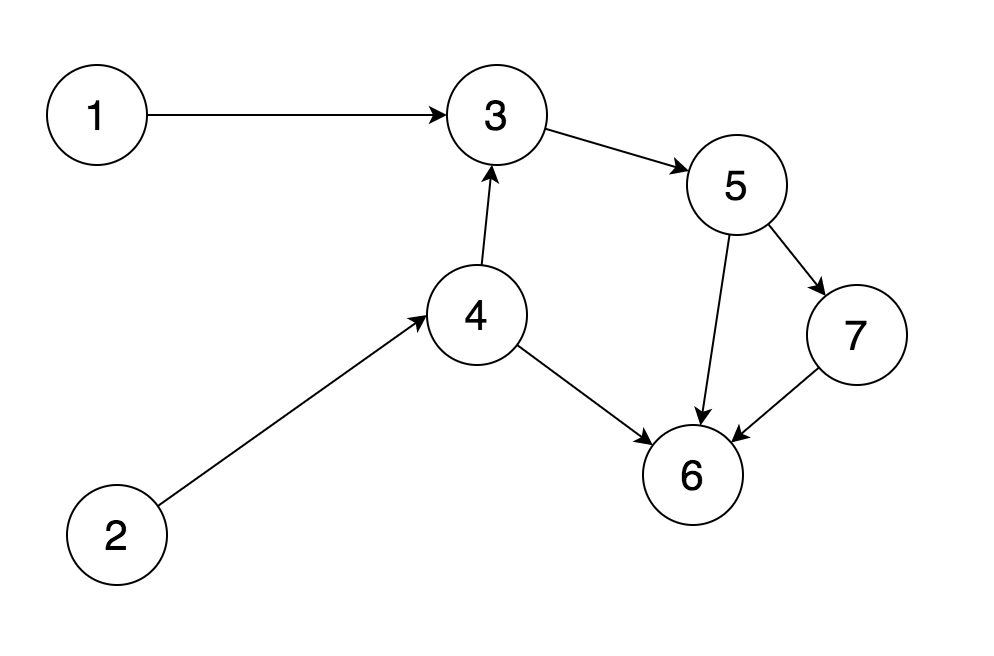
其中, 1 -> 3 表示任务 3 必须在任务 1 完成之后才能够开始。如上图中，任务 3 必须在任务 1 和任务 4 之后。而任务 4 又必须在任务 2 之后。
而要求就是, 提供一个序列，要求按照这个序列能够顺利完成所有任务。这里假设每个时刻只能处理一个任务，而且一旦开始处理某个任务，那么你不能中止或切换到其它任务。这个答案可能不唯一。在上图中，一个可能的答案就是 [1, 2, 4, 3, 5, 7, 6]。
首先有一点是可以确定的：对于任何一连通图，必有一生成树（简直废话）。
对于这一题，关键的问题是确定最大与最小。对于这种寻找两个相关变量的题，其实一般可以先试着确定一个，然后再去寻找另一个。
比如在这题中，可以迭代每一个边 L，同时把这条边 L 当做最小的边，用比它大的边去试着连同一幅图，知道找到边 R， 使得加上这条边 R 后刚好可以凑成一幅联通图。
因此，从上述思路可以看出，排序是必不可少了。所有排序是第一步。
排序好后进行遍历 L，建立 N （顶点数） 个并查集 S，每加入一条边就将该边的端点对应的并查集合并（前提是两个端点对应不同的并查集）。
直到刚好加入边 R 后，并查集只剩一个，且大小刚好与顶点数相等。此时对于 L 来说，R － L 极为其 “苗条度”。
因此对所有求得的“苗条度”求一个最小值即可。如果连一个“苗条度”都没有，那结果自然就是找不到合适的答案了。
假设从( x, y )出发，并且从( x, y )出发所能走的最长路为 d[x][y]，那么设想如果( x - 1, y )的值（即题目所给的高度）要小于(x，y)，那么d[x-1][y] + 1 有可能就是我们所要求的d[x][y]，因为这条路是单向的，只可能从较小的(x-1， y)走向(x，y)。如果考虑四个方向，用(x’， y’)表示(x ， y)上下左右四个方向，那么d[x][y] = max(d[x’][y’]) + 1，且 (x’, y’)上的值要小于(x, y)。那么从这个方程可以看出这实际上可以采用 DFS 加上 dp 的做法，或者称之为记忆化搜索。而 搜索 的终点则是某点(x, y)的四周都比他大，则返回 1。
注意: 这篇文章我曾于 2015 年 5 月 2 日发表在 CnBlog 上。因为那个 blog 我已经几乎不维护，所以准备把部分文章转移至这里。另外，因为那时我还没有在 GitHub 上建立站点，所以这篇文章的发表时间早于这个站点的最早搭建时间。
上个月26号，我有幸参加了今年的浙江省省赛。第一次参加正式的ACM比赛，心里略有点小激动。我的队友们也是第一次参加，还好同行的还有学长学姐们的队伍。
